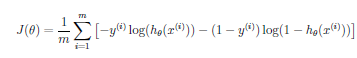
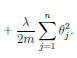
Not all data fits well to a straight line. This is called "underfitting"
or we may say that the algorithm as a "high bias". We can try fitting a quadratic
or even higher order equation. E.g. instead of
O0 + O1x, we might
use O0 + O1x +
O2x2. But, if we choose to use to
high an order equation, then we might "overfit" or have an algorithm with
"high variance", which would fit any function and isn't representing the
function behind this data. Overfitting can therefore result in predictions
for new examples which are not accurate even though it exactly predicts the
data in the trianing set. The training data may well have some noise, or
outliers, which are not actually representative of the true function.
If the data is in 2 or 3 features, it can be plotted and a human can decide if it is being over or under fit. But when there are many parameters, it can be impossible to plot. And using a human is sort of against the purpose of Machine Learning. It may help to reduce the number of features if we can find features that don't really apply. Another means of reducing overfitting is regularization.
We can reduce, but not eliminate, the presence of some terms, by multiplying thier parameter values by a large number and adding that to the cost function. Note this is NOT adding the parameter times the data, but only the parameter itself. The only way the cost can be minimized, in that case, is if the parameter values are small. And if the parameter is small, the term will have less effect on the fit. So we can include higher order terms, without overfitting.
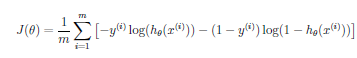
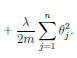
Question: Shouldn't we use lower weight parameters (more regularization) for higher order terms?
Don't regularize O0. There are two ways to avoid
O0 in Octave or other languages: 1. Make a copy
of theta, and set the first element to 0 (memory hungry), then use that copy
when computing the regularization. 2. use theta(2:end) to select
a "slice" of the vector without O0 (can be optimized
depending on the language).
Lambda is used as a parameter for the amount of regularization. e.g. the amount that the parameter values are multiplied by before adding them to the cost function. To large a lambda can result in underfitting. In Octave:
reg = lambda * sum(theta2.^2) / (2*m); J = J + reg; ... reg = lambda .* theta2 ./ m ; S = S + reg;
Where theta2 is either:
theta2 = theta; theta2(1) = 0;
Or
[0; theta(2:end)]
(the [0; and ] aren't needed for the cost calculation, only for the gradient / slope.
Also: