
Variables Whose Values Are Strings
W D Maurer
University Library Building
George Washington University
Washington DC 20052
Almost every programmer has wanted to write a program in which there were
one or more variables with strings as their values. Many programmers, however,
are discouraged by the programming difficulties that arise in this connection,
in all but the simplest cases. This is particularly true when space is at
a premium and assembly language is used as it is in many microcomputer
applications. We would like to describe here two alternative ways of solving
these problems. These are quite different from each other stylistically;
each is fascinating in its own way, and each has certain difficulties which
have to be surmounted, but either one of them will solve the basic problem
with which we are concerned.
Many versions of FORTRAN allow variables to have strings as their values,
but these strings cannot have lengths which are greater than some maximum,
and this maximum is usually much too small for practical purposes. The maximum
is, in fact, the number of characters in a word, which is usually two, four
or six; sometimes it is five (as on the PDP-10) and sometimes eight (as on
the IBM 370, using double words), but in practice the strings we are concerned
with are often 20, 40 or even 60 characters long. In many COBOL programs,
this problem is taken care of by assigning some large number of characters
to every such variable. This is particularly common when the value of the
variable is somebody's name and address, to be printed on an envelope by
the computer. Often 25 characters are rcserved for the name, 25 for the address,
and 25 for the city, state and zip code. This gives rise to two kinds of
problems. In the first place, 25 characters is not enough for an address
like 1527 San Jose-Los Gatos Rd., even if we leave the period off the end.
More important, however, is the fact that, if we reserve that many characters
for every name and every address, there are going to be quite a lot of wasted
characters. That doesn't matter too much in a COBOL program, where space,
particularly on a disk, is usually quite abundant; but on a micro- computer
we would like to make optimum use of all the space we have.
The first solution to this problem that we will consider involves the use
of a large array, called SPACE, for the storage of strings. Let us consider
each element of this array to be one character long. Then the first string
(whose length is L1, say) is stored in the characters SPACE (1), SPACE(2)
and so on up through SPACE(L1). The next character, SPACE(L1+1), contains
an illegal character code (zero, for example) to denote the fact that this
is the end of the first string. The second string starts at SPACE(L1+2) and
continues from there. Every string ends with a zero character code, and all
the strings are stored in the array called SPACE, in sequential order. Suppose
now that these strings are supposed to be the values of variables K1, K2
and so on in the program. The actual value of each of these variables will
be an integer that indicates where the corres- ponding string starts. Thus,
for example, if 17 is the value of K2, then SPACE(17) is the first character
of the given string; SPACE(18) is the next character, and so on. This is
the basic concept of a pointer: a quantity which indicates where another
quantity is in memory. The pointers we have set up have been index pointers,
but it would have been just as easy to set up address pointers. That is,
instead of the integer 17, we could have used the address, in memory, of
the character SPACE(17). The basic problem that arises when this method is
used can be seen if we consider the process of setting a variable to a new
value.
Suppose that the value of K1 is 'SMlTH' and we want to change it to 'JOHNSON'.
Unfortunately, 'JOHNSON' has more letters in it than 'SMITH', so we cannot
simply store the new characters in the same places as we stored the old ones.
We can, however, take advantage of the fact that not all of our array SPACE
has been used. Suppose that we have used the characters from SPACE(1) up
through SPACE(LSPACE); then 'JOHNSON' can start at SPACE(LSPACE+1), and we
can set the pointer in K1 to be LSPACE+1. Of course, we also have to update
LSPACE at this point, by adding to it the length of JOHNSON, or 7 (plus 1,
for the zero character) . The trouble with this method is that now SMITH
is still in memory, together with its zero character. We are not really using
all the space from SPACE(1 ) up through SPACE(LSPACE); there are five characters,
plus a zero character, that we are not using. By itself this causes no problems;
but now consider what happens as our program continues to run. Every time
we have a variable with a string as its value, and this variable gets a new
string as its value, we are going to "abandon" some of our string storage
area, just as we did with SMITH in this case. Eventually, we are going to
run out of space; the whole SPACE array will be used up, except for "abandoned"
areas as above. What do we do next? Let us agree that, whenever we abandon
a string, we write a zero character over the first character of that string.
This character will immediately follow the zero character at the end of the
preceding string, so that two zero characters in a row will denote the start
of an abandoned area. We can now consider the possibility of moving all the
strings backwards by just enough so that the abandoned areas disappear, as
shown in figure 1. This is known as collapsing (or sometimes compactifying).
If we think of the left side of figure 1 as a row of bricks, with spaces
between them to represent the abandoned areas, then putting our hands on
the two ends of the row and collapsing it would produce the situation shown
in the right side of the figure. An algorithm to do this involves two pointers,
I and J. As we move each character in SPACE, we set SPACE(J) = SPACE(I),
and then add 1 to both I and J. When we have to skip over an abandoned area,
we increase 1, but not J. Thus I always indicates the current character we
are moving, and J always indicates the place we are moving it. At the start
of the algorithm, both I and J are initialized to 1. There is still one
difficulty.
All our variables with string values involve pointers, and after the collapsing
process has taken place, the pointers will be wrong. We have to have some
way of adjusting these pointer values. There are at least two reasonable
ways of doing this. One of these involves what may be called back pointers.
The first character (or possibly the first two characters) of each string,
as given in the array SPACE, is now some indication of which variable has
this particular string as its value (such as, for example, the address of
that variable). Whenever a back pointer is moved, by the operation SPACE(J)
= SPACE(I), we look in that position (which should contain 1) and change
it to J. The other method involves a sorting operation. All the pointers
that are contained in all the variables with string values are placed in
an array and sorted in ascending order, together with back pointers to the
given variables. As we are going through the SPACE array and setting SPACE(J)
= SPACE(I), we are also going through this new array, from the beginning
to the end. At each stage, the pointer in this array that we are currently
considering points to the place in the SPACE array that we will have to treat
next, as the start of a string to be moved. When we get to this point in
SPACE, we reference the associated back pointer and proceed as before; then
we continue through the SPACE array, but also move forward by one position
in the new array, so that we will be ready to treat that pointer when we
come to it.
Let us now pass to the second method of handling string values of variables.
Again we use a large array, which we will call FREE this time, rather than
SPACE. FREE is organized into groups of characters; to make our example concrete,
we will assume that each group is eight characters long. The first six of
these characters are actually characters of the given string; the remaining
two character positions, taken together, contain a pointer to another group
of eight characters. Any string which is less than six char- acters long
is stored in a single group. If a string is four characters long, for example,
the last two characters are zero characters; this tells us that these are
not actually to be counted as part of the string. A string which is more
than six characters long is stored as a chain. Thus, for example, if a string
is 15 characters long, the first six of these characters appear in one group,
which contains a pointer to another group. The next six characters appear
in this second group, which contains a pointer to a third group. The last
three characters appear in the third group, followed by three zero characters.
If a string is exactly six characters long, it appears in a single group,
but the pointer itself contains zero. If a string is 12, 18, 24, etc, characters
long, it appears in more than one group, but the pointer in the last group
will contain zero. In general, the pointer in the last group always contains
zero, and it is this, rather than the presence of zero char- acters, that
determines the fact that it is the last group. We thus have one or more chains
(sometimes called simple lists) which involve various 8 character groups
in FREE.
We are now in a position to make use of a basic idea in advanced programming
techniques: the list of available space. In this case, the list of available
space is a chain which con- tains all those 8 character groups, and only
those groups, which are not on any other chain. That is, we think of all
these groups as being in some order (it does not matter what the order is).
Then the first group, in this order, contains a pointer to the second group;
the second group contains a pointer to the third, and so on, up to the last
group, which contains a zero pointer. The point of using a list of available
space is that it is now no longer necessary to use a collapsing process,
as described in con- nection with the previous string storage method. In
particular, we are no longer "abandoning" anything, as we were before. All
we have to do is to make sure that, at all times, every group into which
FREE is divided is on some chain, either the list of available space, or
a chain which represents the string value of some variable. (There are also
programs which use a list of available space, but in which some groups are
abandoned, and a process somewhat like collapsing, known as garbage collection,
is used to collect all these abandoned groups into a new list of available
space. This, however, is necessary only when the various chains contain pointers
to each other, which is not the case in the present application.) By a pointer
to a group, we mean a pointer to the first character in the group. Thus if
Kis such a pointer, then the group consists of FREE(K), FREE(K+l) and so
on up through FREE(K+7). We will assume that FREE(K) through FREE(K+5) are
the six characters in the group, and that FREE(K+6) and FREE(K+7), taken
together, are the pointer to the next group. A variable called LAVS (for
"list of available space") contains, at all times, a pointer to the first
group in the list of available space. The basic operations on the list of
available space are taking one group off the front of it and adding a new
group to it.
The first of these operations, removing a group from the list of available
space, is performed as follows:
-
Set K = LAVS; the new group wich consists of FREE(K) through FREE(K+7).
-
Since this group is no longer to be on the list of available space, the first
group in this list is now what used to be the second group. But a pointer
to this second group is currently in FREE(K+6) and FREE(K+7). This pointer
now has to be taken and put into LAVS, because LAVS must contain, at all
times, a pointer to the first group in the list of available space.
The second of our two operations, adding a group to the list of available
space, is performed as follows:
-
Suppose that FREE(K) through FREE(K+7) is the new group. This will become
the first group in the list of available space, and it must contain
a pointer to the second group. But the second group is the old first
group and a pointer to that group was contained in LAVS. This means that
LAVS must be moved into the point position FREE(K+6) and FREE(K+7)
-
Since LAVS must contain, at all times a pointer to the first group in the
list of available space, we must now set LAVS equal to K.
The first operation above can be modified to check for overflow. If it is
performed when the list of available space contains exactly one group, it
is not hard to see that LAVS will be set equal to zero. This is not in itself
an error; it merely means that all available space is being used. The next
time we do this, though, there will be an error unless we check for it.
Therefore, when we set K = LAVS, we should check to see if K is now zero;
if so, there is an overflow condition. (We are, of course, using the word
"overflow" in a generalized sense, to denote the fact that there is too much
space being used for the available memory in the FREE array.) Using these
two basic operations, we can now make sure that our available space list
is always kept up to date. Suppose that we have a variable J with a string
value, and suppose that this string value is kept in m 8 bit groups. A pointer
to the first of these groups will be kept in J itself. Suppose that we are
now going to set J to a new string value, which is kept in n 8 bit groups.
First we apply the second algorithm above to the first group in the chain
that represents the old value of J. This process puts this group on the list
of available space. If m~1, that is, if the pointer in this first group was
not originally zero, we apply the same process to the second group in the
chain representing the old value of J, and so on through the rest of these
groups. (It is not necessary to know m, of course; we merely test for the
pointer being zero, which indicates the last group.) Now we take n groups,
or, in general, as many groups as we need, off the front of the list of available
space by using the first algorithm above, and use these groups to store the
new string value of J.
This system is quite workable as it stands; the only real problems with it
come when we try to extend it. Suppose, for example, that we want to set
the string value of J equal to the current string value of 1. In that case
we might want to save quite a bit of time by setting the pointer in J to
be the same as the pointer in 1. Thus we would have two pointers to the same
group, or to the first group of the same chain, in the FREE area. This scheme,
however, will not work unless we change our setup a bit. The problem comes
when the value of I is later changed to something else. In this case the
old value of I is put back on the list of available space, and this is improper
because it is still the current value of J. Let us look at this case in more
detail. Suppose that the value of I is 'SMITH ', and we set J equal to 'SMITH'
by setting J to point to the same place that I does. Now suppose that we
later set I equal to 'JOHNSON'. In this case, according to the algorithms
we have discussed, the group [there is only one in this case; let us call
it FREE(K) through FREE(K+7)] which contains 'SMITH ' is put back on the
list of available space, even though K is still the integer value of J. Now
we need two groups to represent 'JOHNSON'. One of these will be this same
group, that is, FREE(K) through FREE(K+7), because it was just put back on
the beginning of the list of available space. This group will therefore contain
JOHNSO (with the final N in the next group). This means that if at some still
later time we want to print out the value of J, we will print out JOHNSON
rather than SMITH. One solution to this problem which is sometimes adopted
is to reserve the first character of any string for a special integer telling
us how many variables have this particular string as their value. This integer
is known as a reference count. It is usually 1, but in the case above (where
J and I point to the same string) it would be 2. Every time a variable is
set to a new value, the reference count in the old value is decreased by
1. Only if its value is then zero do we return the space it uses back to
the list of available space, because otherwise there are still variables
which have that string as their value. The trouble with this scheme is that
it may very easily not be worth the effort. Do we really want to add an extra
character to every string, not to mention the extra testing that goes on
whenever we set a string to a new value, just to be able to save a little
time and space in an operation (setting one string to be the same as another)
that might not be that commonly used in our program? It is certainly a debatable
point. It should also be clear that there is nothing special about the number
of char- acters in a group (eight, in this case). The fewer characters we
have in a group, the more pointers we will have, and the more space these
will take up. The more char- acters we have in a group, the more wasted or
zero characters we will have in strings, because the length of a string is
not always evenly divisible by the number of characters in a group. This
is a space trade-off which should be tuned by the user to fit the requirements
of a particular program.
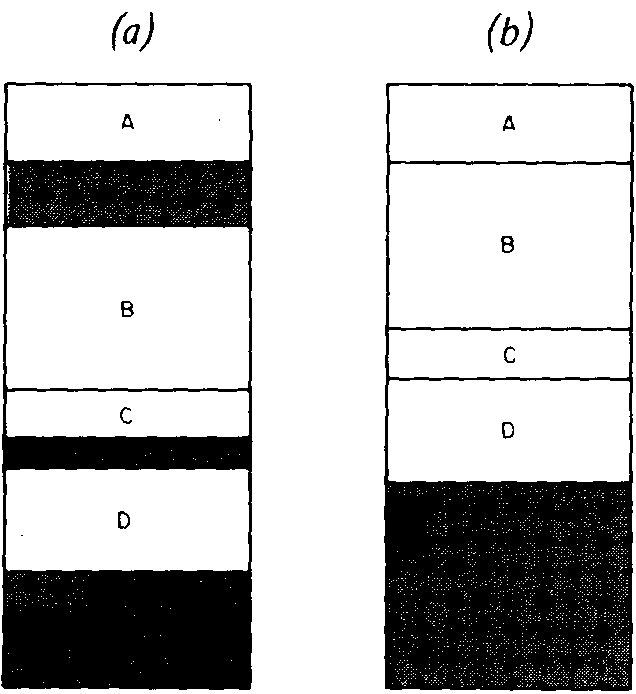 Figure
1: Collapsing or "compactifying" an array. In figure 1a A, B, C and D are
separated by empty space (shaded area). In figure 1b this empty, available
space is consolidated by moving B, C and D up so that they are contiguous
with A. Whenever we abandon a string, we write a zero character over the
first character of that string so we can go back later and identify the string
as abandoned .
Figure
1: Collapsing or "compactifying" an array. In figure 1a A, B, C and D are
separated by empty space (shaded area). In figure 1b this empty, available
space is consolidated by moving B, C and D up so that they are contiguous
with A. Whenever we abandon a string, we write a zero character over the
first character of that string so we can go back later and identify the string
as abandoned .
file: /Techref/method/string/strings.htm, 18KB, , updated: 1999/2/20 13:29, local time: 2025/10/2 19:23,
216.73.216.49,10-1-111-198:LOG IN
|
| | ©2025 These pages are served without commercial sponsorship. (No popup ads, etc...).Bandwidth abuse increases hosting cost forcing sponsorship or shutdown. This server aggressively defends against automated copying for any reason including offline viewing, duplication, etc... Please respect this requirement and DO NOT RIP THIS SITE. Questions?
<A HREF="http://massmind.org/techref/method/string/strings.htm"> Variables Whose Values Are Strings</A> |
| Did you find what you needed?
|
.
 Figure
1: Collapsing or "compactifying" an array. In figure 1a A, B, C and D are
separated by empty space (shaded area). In figure 1b this empty, available
space is consolidated by moving B, C and D up so that they are contiguous
with A. Whenever we abandon a string, we write a zero character over the
first character of that string so we can go back later and identify the string
as abandoned .
Figure
1: Collapsing or "compactifying" an array. In figure 1a A, B, C and D are
separated by empty space (shaded area). In figure 1b this empty, available
space is consolidated by moving B, C and D up so that they are contiguous
with A. Whenever we abandon a string, we write a zero character over the
first character of that string so we can go back later and identify the string
as abandoned .