
 コンデンサの周波数特性 コンデンサの周波数特性
抵抗器は周波数が変化しても抵抗値は変化しませんが、コンデンサに交流信号を加えると周波数により抵抗値が変化します。このコンデンサの抵抗値は容量リアクタンスと呼ばれています。
記号ではZが使われ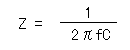 になります。 になります。
例えば0.01μFの容量をもつコンデンサに1KHzの交流信号をかけた場合のリアクタンス(抵抗値)は以下のようになります。
抵抗器もコンデンサも理想的なものはありません。(実際の部品は理論上のものとは違うという意味です)
抵抗器も少ないですがコイルおよびコンデンサの成分があります。ですから、周波数が高くなると抵抗器も種類によってはコイルおよびコンデンサの成分が影響して抵抗値が変わってしまいます。この影響が問題となるような周波数を扱う回路では高周波用抵抗器を使う必要があります。
コンデンサも同じで純粋な容量成分(Capacitance)だけではなく、抵抗成分(Resistance)およびコイル成分(Inductance)があります。特にコンデンサの場合、電極を巻いた構造をしているものはコイル成分が多く高い周波数では使えません。

 コンデンサと抵抗器の組み合わせによる合成抵抗 ( インピーダンス ) コンデンサと抵抗器の組み合わせによる合成抵抗 ( インピーダンス )
 直列接続 直列接続
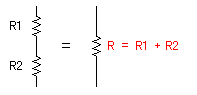
抵抗器R1とR2を直列に接続したときの合成抵抗はR1+R2です。
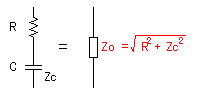
抵抗器R1とコンデンサ(Zc)を直列に接続した場合の合成抵抗は単に加算では求められません。
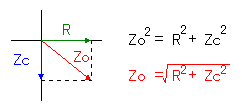 それはコンデンサの場合、コンデンサに加わる電圧とコンデンサに流れる電流の位相が90度ずれるためです。合成抵抗はピタゴラスの定理を使用して計算する必要があります。直角三角形の長辺を求めるわけです。 それはコンデンサの場合、コンデンサに加わる電圧とコンデンサに流れる電流の位相が90度ずれるためです。合成抵抗はピタゴラスの定理を使用して計算する必要があります。直角三角形の長辺を求めるわけです。
実際の合成抵抗の計算式は以下のようになります。
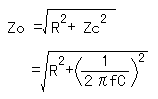
 並列接続 並列接続
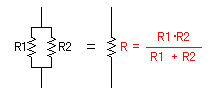
抵抗器R1とR2を並列に接続したときの合成抵抗はR1 x R2/(R1+R2)です。
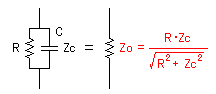
抵抗器Rとコンデンサ(Zc)を並列に接続した場合は左図のようになります。
実際の合成抵抗の計算式は以下のようになります。
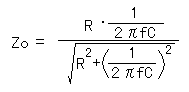
面倒なことを説明しましたが、上記の接続が微分回路、積分回路で使われています。

 微分回路および積分回路におけるカットオフ周波数での減衰量 微分回路および積分回路におけるカットオフ周波数での減衰量
 微分回路 微分回路
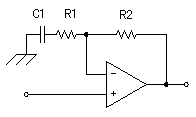
抵抗器(R1)とコンデンサ(C1)により微分回路の特性が決まります。
カットオフ周波数でのC1とR1によるインピーダンスを計算すると以下のようになります。
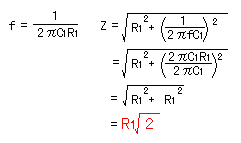
このときオペアンプのゲインは以下のようになります。
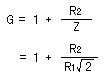
すなわち、カットオフ周波数より高い周波数のゲインの約0.7倍になります。
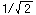 をデシベルで表すと以下のようになります。
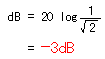
 積分回路 積分回路
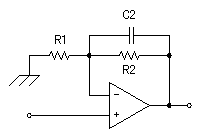
抵抗器(R2)とコンデンサ(C2)により積分回路の特性が決まります。
カットオフ周波数でのC2とR2によるインピーダンスを計算すると以下のようになります。
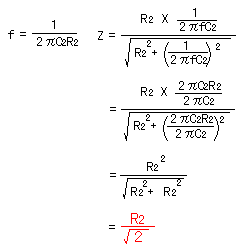
このときオペアンプのゲインは以下のようになります。
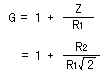
すなわち、カットオフ周波数より低い周波数のゲインの約0.7倍になります。
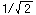 をデシベルで表すと以下のようになります。
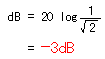 微分回路も積分回路もカットオフ周波数では−3dBゲインが落ちることになります。
微分回路も積分回路もカットオフ周波数では−3dBゲインが落ちることになります。
 |